In the previous post “Introducing the Action Framework”, we presented a separate architecture where behaviours act as reactors to the current state of the game. This allows active behaviours to run synchronously and quickly, moving the more “deliberate” processing to a separate thread or fiber. But how do we select our behaviours? FSMs, trees, planners, as discussed previously?
(UPDATE: the previous post not only owes to the CERA architecture, as we will see later, but also Carle Côté’s article on “Reactivity and Deliberation in Decision-Making Systems” in the Game AI Pro book. Browsing this title has also shown that the choice of title, as well as some inspiration, has been drawn from Bill Merrill’s article, “Building Utility Decisions into Your Existing Behavior Tree”.)
Trees for Funs
In the last nucl.ai, recent developments in behaviour trees arose a number of comments from the attendants about how nodes in a behaviour tree are becoming more similar to functions in a more traditional programming language, and why there was not more general programming support in behaviour trees. After some thinking, we believe that general programming languages are far too complex and varied to be useful as they are. Some sort of constrained, simpler execution model would be much more useful to AI programmers (that can build more powerful tools themselves if need be) and AI authors (that do not need to learn several programming languages to come up with sensible AI). But we also believe that a good model for behaviours need not mimic any of the existing constructs in programming languages. Why and how? Let’s take a look at the current approach.
From Trees to Sprouts
A behaviour tree in many current tools looks like this:
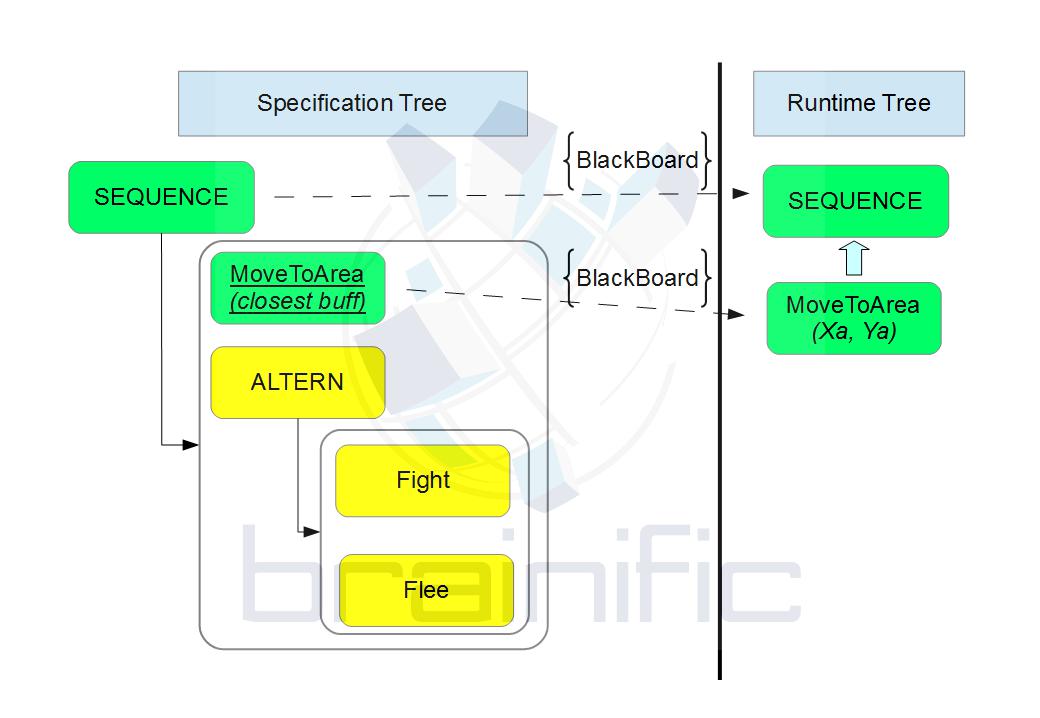
You can see active nodes in green, and non-active nodes in red. This might seem enough at first. However, we have realized that separating the specification data from the runtime data provides much more flexibility at little cost. We can visualize this separation in the following drawing:
Effectively, we have a specification part, that tells us how new nodes are generated in the runtime part; and a runtime part, that looks suspiciously similar to a function stack (and it works as one, as well; but there are some differences). Note the word “generated”. New runtime nodes are instantiated from the parent node, which is in turn an instantiation of some kind of “prototype” node, or a lambda, or a factory. In our case, a sequence node inserts itself in the runtime tree, and spawns another node as a child.
The important point is that the structure does not need to have a one-to-one correspondence to the runtime node tree. It only generates this runtime tree using some rules. In the following examples we will use mainly Haskell to illustrate these rules and they way we can twist and enrich them, but many of these mechanisms can be implemented in other languages (albeit much less succintly).
Before jumping to an example, let us be honest: this is not new at all. Whether consciously or by chance, we are replicating the mechanisms sketched by Mateas and Stern in their article “A Behavior Language: Joint Actions and Behavioral Idioms” about the tools used in their game, Façade. The authors even speak about generating appropriate behaviors according to preconditions, so basically they are unifying behavior trees and some kind of hierarchical, no backtracking, contingent planning. One of the differences is that we have separated the behaviour active part from its planning part. Once a behaviour becomes active, it reacts to everything coming from the game world, until the planning layer removes it from play. Even if this means skipping a couple of frames when thinking what to do next, behaviours become simpler to understand: if the state is like this, we do like that. When some conditions are met, then we think for a frame or two what is the next action, change the active behaviors after acting for the frame and off we go again.
But let us be even more honest. Not even the idea of separating a lower and an upper layer is really ours. It bears enough resemblance to Raúl Arrabales and Jorge Muñoz’ CERA-CRANIUM architecture for their award-winning UT bot “Conscious Robots”. We think that our only merit here is to streamline both ideas and use an appropriate tool (Haskell, in this case) to better provide these capabilities to a game programmer.
An Easy Patrol
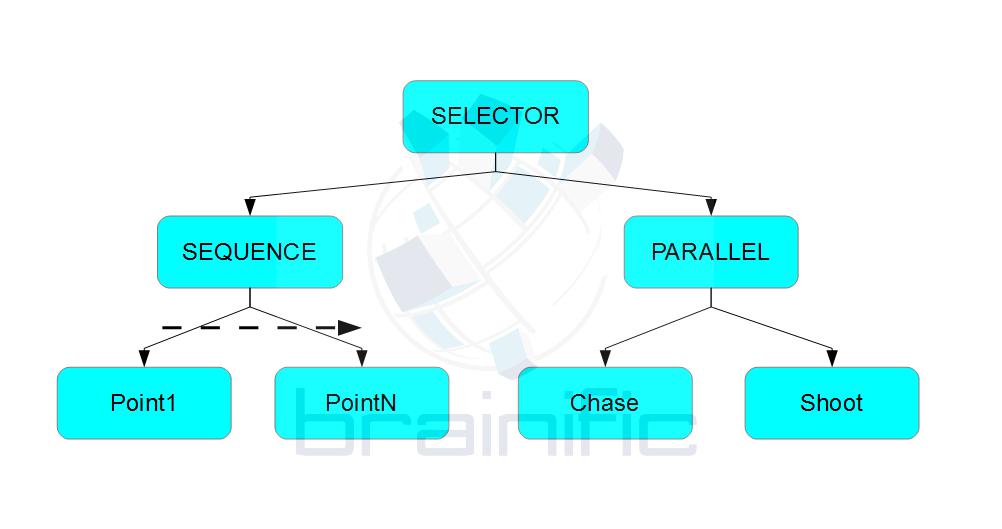
We will illustrate this separation between specification and runtime parts in an example. Our first task will be to specify a patrol behaviour. With the current state of the art, one would draw a sequence tree, with some kind of “loop” modifier since we need the patrol to run forever. If the patrol fails (by, say, spotting an enemy), then an alternate tree will spawn that activates behaviours for chasing and shooting the target. It would look something like this:
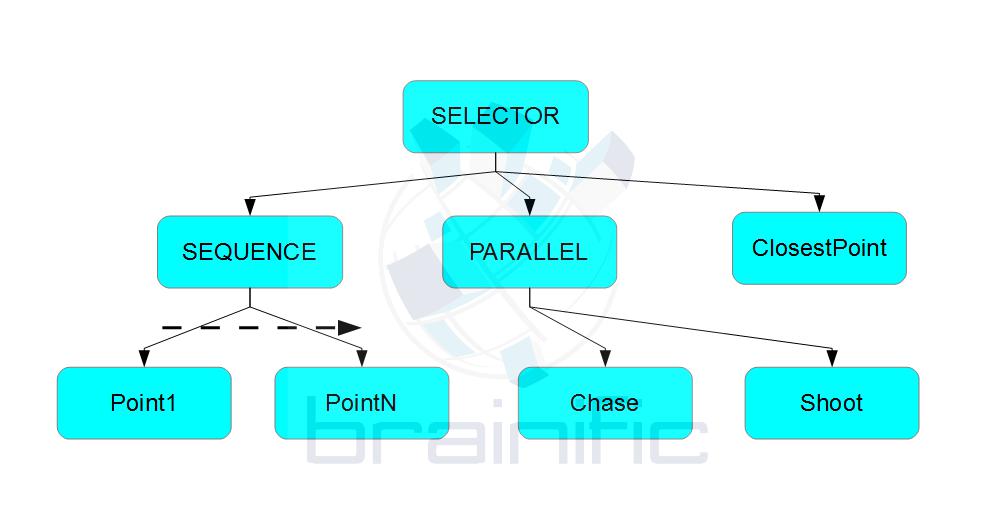
Our first issue is that, after the chase, we want to start the patrol, but not starting in the first point in the specified patrol, but instead in the closest point to the patrol. Repeating the patrol from the farthest end would not look very intelligent, right? So we modify our tree to look something like this:
One issue with this approach is that the runtime view now differs from the specification view: whereas the specification view says “move to the closest point” (and needs to check the blackboard), the runtime view knows the point towards which we are heading, and it will not change. Current behaviour trees can cope with this situation with little changes.
But we want to make our game much more flexible. Take into account that, even if we move to the closest point in the patrol, we need to specify where in the patrol we start. Now our sequence node needs to have some additional list-specific code that modifies the sequence. The separation of specification and runtime views comes in handy at this point.
Instead of moving to a predefined set of points (first go to XaYa, then to XbYb…), we want to specify these points at runtime. As we said, the specification view will handle node spawns (or factories) whereas the runtime view will always handle proper nodes. The specification can say, “this node spawn will take a BlackBoard and issue a Sequence node holding the shortest prefix of the patrol list”. However complicated we want to make the specification, it will nonetheless will be a Sequence node spawning MoveBehaviour nodes at runtime. The specification and runtime views would look something like this.
We will make a function (or a factory, or whatnot) that returns a sequence node using a BlackBoard:
data SeqNode = SeqNode NodeId (forall n. (Node n) => [n])
type seqNodeSpawn = BlackBoard -> SeqNode
patrolPoints = [(0,0), (3,3), (8,8), (10,10)]
prePatrolNodeSpawn = runFromCloserSeqNode "prepatrol" patrolPoints
cycleMoveNodeSpawn = runSeqNode "patrol" $ moveSpawnList $ cycle patrolPoints
patrolNodeSpawn = runSeqNode "complete_patrol" [prePatrolNodeSpawn, cycleMoveNodeSpawn]
You can find all the source code in bitbucket; please take into account that this is WIP, and is appropriately dirty and badly structured for the moment.
(Haskellers out there: the definition of the SeqNode has some complexities that we decided to leave out. For the complete datatype specification, using a “generic node” that holds the specific type of the type class and that performs the polymorphic action, refer to the source code . A profane probably understands it better like this.)
The “runSeqNode” spawn creates a sequence node from a blackboard. It takes an ID and a node spawn list (note that each node spawn will create a node from the data in the blackboard and insert it in the runtime tree under the parent node). One interesting feature in Haskell is that we can easily use and handle infinite lists: the cycle function takes a finite list and repeats it to make it infinite. One drawback is that we can no longer write the list of children, but instead we need to make “event runs” or “event traces” an inspect the runtime trees they create. The auxiliary function “moveSpawnList” takes a list of positions and turns them into Move behaviours for those positions:
moveSpawnList posList = moveBehavioursList
where
moveId = (++) "move-" . show
moveBehavioursList = map (\x -> runBehNode (moveId x) (moveBehaviour x)) posList
The “runBehNode” spawn, as expected, creates a behaviour node with an ID and an associated low level behaviour (see our previous post and remember that behaviours are properly reactive, always-on actions that produce actions with each frame).
In our second approach, we needed to find the closest point in the patrol list. How would we do this in this “separated” framework? We need a move behaviour spawn that creates a runtime node depending on values of the BlackBoard:
runMoveToCloserNode id posList (mem, bb) | length posList > 0 = (runTree, behaviours)
where
BlackBoard _ _ _ curPos _ _ _ = bb
runTree = Node (GenNode $ BehaviourNode id) []
closeList = [(p, d p curPos) | p <- posList]
d (x1,y1) (x2,y2) = (x1-x2)*(x1-x2) + (y1-y2)*(y1-y2)
(closest, _) = foldl1' (\tmin@(pmin,dmin) t@(p,d) -> if d<dmin then t else tmin) closeList
behaviours = [moveBehaviour closest]
We fold the values of (un-square-rooted) distances to find out the closest point, and then issue a behaviour move with the right point. Finding out the prefix is somewhat more complex, but equally compact:
runFromCloserSeqNode id posList env@(mem, bb) | length posList > 0 = (runTree, behaviours)
where
BlackBoard _ _ _ curPos _ _ _ = bb
d (x1,y1) (x2,y2) = (x1-x2)*(x1-x2) + (y1-y2)*(y1-y2)
pointSubListDistList = unfoldr (\x -> case x of [] -> Nothing; l@(p:xs) -> Just ((p,l,d p curPos),xs)) posList
(closest, closestSubList, _) = foldl1' (\tmin@(pmin,smin,dmin) t@(p,s,d) -> if d<dmin then t else tmin) pointSubListDistList
spawnList = moveSpawnList closestSubList
firstSp = head spawnList
restSp = tail spawnList
runTree = Node (GenNode $ SeqNode id restSp) [nextTree]
(nextTree, behaviours) = firstSp env
We create a list of patrol points, with their distance values and suffixes. We find out the closest point, and then generate a list of behaviours that the sequence node spawn will use. When spawned, this sequence node gets inserted in the runtime tree, running the first move spawn node and inserting it underneath it, and holds the rest of spawns. Note that, at each point where a node needs to handle an event (success or failure), the node accesses the blackboard and generates new runtime nodes with this information.
We now how to spawn new nodes in response to events, but the only event we have now is the “start” event. In a following post we will introduce event handling along the runtime tree, including some areas where the behaviour of the system is still undefined. We will also explain how the separation of specification and runtime trees allows us to handle FSMs more naturally using a common framework, and why the usual “function call” abstraction is not powerful enough to implement this framework. Stay tuned!!!!